Last time on FAIC we reviewed the meaning of “expected value”: when you get a whole bunch of samples from a distribution, and a function on those samples, what is the average value of the function’s value as the number of samples gets large?
I gave a naive implementation:
public static double ExpectedValue<T>(
this IDistribution<T> d,
Func<T, double> f) =>
d.Samples().Take(1000).Select(f).Average();
public static double ExpectedValue(
this IDistribution<double> d) =>
d.ExpectedValue(x=>x);
Though short and sweet, this implementation has some problems; the most obvious one is that hard-coded 1000 in there; where did it come from? Nowhere in particular, that’s where.
It seems highly likely that this is either too big, and we can compute a good estimate in fewer samples, or that it is too small, and we’re missing some important values.
Let’s explore a scenario where the number of samples is too small. The scenario will be contrived, but not entirely unrealistic.
Let’s suppose we have an investment strategy; we invest a certain amount of money with this strategy, and when the strategy is complete, we have either more or less money than we started with. To simplify things, let’s say that the “outcome” of this strategy is just a number between 0.0 and 1.0; 0.0 indicates that the strategy has completely failed, resulting in a loss, and 1.0 indicates that the strategy has completely succeeded, resulting in the maximum possible return.
Before we go on, I want to talk a bit about that “resulting in a loss” part. If you’re a normal, sensible investor like me and you have $100 to invest, you buy a stock or a mutual fund for $100 because you believe it will increase in value. If it goes up to $110 you sell it and pocket the $10 profit. If it goes down to $90, you sell it and take the $10 loss. But in no case do you ever lose more than the $100 you invested. (Though of course you do pay fees on each trade whether it goes up or down; let’s suppose those are negligible.) Our goal is to get that 10% return on investment.
Now consider the following much riskier strategy for spending $100 to speculate in the market: suppose there is a stock currently at $100 which we believe will go down, not up. We borrow a hundred shares from someone willing to lend them to us, and sell them for $10000. We pay the lender $100 interest for their trouble. Now if the stock goes down to $90, we buy the hundred shares back for $9000, return them to the owner, and we’ve spent $100 but received $1000; we’ve made a 900% return on the $100 we “invested”. This is a “short sale”, and as you can see, you get a 900% return instead of a 10% return.
(I say “invested” in scare quotes because this isn’t really investing; it’s speculation. Which is a genteel word for “gambling”.)
But perhaps you also see the danger here. Suppose the stock goes down but only to $99.50. We buy back the shares for $9950, and we’ve only gained $50 on the trade, so we’ve lost half of our $100; in the “long” strategy, we would only have lost fifty cents; your losses can easily be bigger with the short strategy than with the long strategy.
But worse, what if the stock goes up to $110. We have to buy back those shares for $11000, so we’ve “invested” $100 and gotten a “return” of -$1000, for a total loss of $1100 on a $100 investment. In a short sale if things go catastrophically wrong you can end up losing more than your original investment. A lot more!
As I often say, foreshadowing is the sign of a quality blog; let’s continue with our example.
We have a process that produces values from 0.0 to 1.0 that indicates the “success level” of the strategy. What is the distribution of success level? Let’s suppose it’s a straightforward bell-shaped curve with the mean on the “success” side:

This is a PDF, and extra bonus, it is normalized: the total area under the curve is 1.0. The vast majority of the time — 99.9% — our investment strategy produces an outcome between 0.48 and 1.0, so that’s the area of the graph I’m going to focus on.
Aside: I know it looks a little weird seeing a bell-shaped curve that just cuts off abruptly at 1.0, but let’s not stress about it. Again, this is a contrived example, and we’ll see why it is irrelevant later.
Now, I don’t intend to imply that the “success level” is the return: I’m not saying that most of the time we get a 75% return. Let’s suppose that we’ve worked out a function that translates “strategy outcome level” to the percentage gain on our investment. That is, if the function is 0.0, we’ve not gained anything but we’ve not lost anything either. If it is 0.5 then our profits are 50% of our investment; if it’s -0.25 then we’ve taken a net loss of 25% of our investment, and so on.
Let’s propose such a function, and zoom in on the right side of the diagram where the 99.9% of cases are found: from 0.46 to 1.0. Here’s our function:
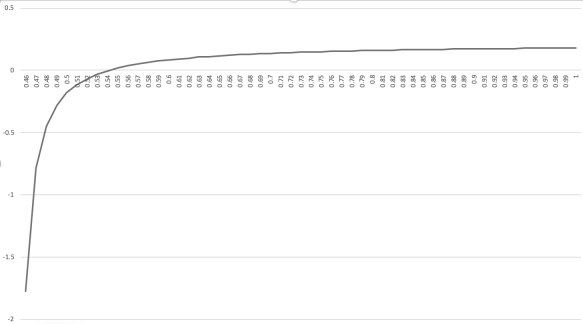
If our process produces an outcome of 0.54 or larger, we make between a 0% and an 18% return, which seems pretty good; after all the vast majority of the bulk of the distribution is to the right of 0.54. Now, in the unlikely case where we get an outcome from 0.48 to 0.54, we lose money; on the left hand end, we’re losing almost 200%; that is, if we put in $100 we not only fail to make it back, we end up owing $100.
The question at hand, of course, is what is the average value of the “profit function” given the distribution of outcomes? That is, if we ran this strategy a thousand times, on average what return would we get?
Well, we already wrote the code, so let’s run it: (Code can be found here.)
var p = Normal.Distribution(0.75, 0.09);
double f(double x) =>
Atan(1000 * (x – .45)) * 20 – 31.2;
Console.WriteLine($”{p.ExpectedValue(f):0.##}“);
Aside: I’m ignoring the fact that if we get a sample out of the normal distribution that is greater than 1.0 or less than 0.0 we do not discard it. The region to the left of 0.0 is absurdly unlikely, and the region to the right of 1.0 has low probability and the value of the profit function is very flat. Writing a lot of fiddly code to correct for this problem would not change the estimated expected value much and would be a distraction from the far deeper problem we’re about to discover.
Also, I’m limiting the distribution to a support of 0.0 to 1.0 for pedagogical reasons; as we’ll see in later episodes, we will eventually remove this restriction, so let’s just ignore it now.
We get the answer:
0.14
Super, we will get on average a 14% return on our investment with this strategy. Seems like a good investment; though we have a small chance of losing big, the much larger chance of getting a solid 0% to 18% return outweighs it. On average.
Aside: It is important to realize that this 14% figure does not necessarily imply that typically we get a 14% return when we run this strategy, any more than the expected value of 3.5 implies that we’ll typically get 3.5 when we roll a d6. The expected value only tells you what the average behaviour is; it doesn’t tell you, for example, what the probability is that you’ll lose everything. It tells you that if you ran this strategy a million times, on average you’d get a 14% return, and that’s all it tells you. Be careful when making decisions relying upon expected values!
This 14% expected result totally makes sense, right? We know most of the time the result will be between 0% and 18%, so 14% seems like a totally reasonable expected value.
As one of my managers at Microsoft used to say: would you bet your car on it?
Let’s just run the code again to be sure.
0.14
Whew. That’s a relief.
You know what they say: doing the same thing twice and expecting different results is the definition of practicing the piano, but I’m still not satisfied. Let’s run it another hundred times:
0.14, 0.08, 0.09, 0.14, 0.08, 0.14, 0.14, 0.07, 0.07, 0.14, ...
Oh dear me.
The expected return of our strategy is usually 14%; why it is sometimes half that? Yes, there is randomness in our algorithm, but surely it should not cause the value computed to vary so widely!
It seems like we cannot rely on this implementation, but why not? The code looks right.
As it turns out, I showed you exactly the wrong part of the graphs above. (Because I am devious.) I showed you the parts that make up 99.9% of the likely cases. Let’s look at the graph of the profit-or-loss function over the whole range of outcomes from 0.0 to 1.0:

OUCH. It’s an approximation of a step function; in the original graph that started at 0.46, we should have noticed that the extremely steep part of the curve was trending downwards to the left at an alarming rate. If you have an outcome of 0.48 from our process, you’re going to lose half your money; 0.46, you lose all your money and a little bit more. But by the time we get to 0.44, we’re down to losing over 60 times your original investment; this is a catastrophic outcome.
How likely is that catastrophic outcome? Let’s zoom in on just that part of the probability distribution. I’ll re-scale the profit function so that they fit on the same graph, so you can see where exactly the step happens:

This is a normalized PDF, so the probability of getting a particular outcome is equal to the area of the region under the curve. The region under the curve from 0.38 to 0.45 is a little less than a triangle with base 0.07 and height 0.02, so its area is in the ballpark of 0.0007. We will generate a sample in that region roughly once every 1400 samples.
But… we’re computing the expected value by taking only a thousand samples, so it is quite likely that we don’t hit this region at all. The expected losses in that tiny area are so enormous that it changes the average every time we do sample from it. Whether you include a -60 value or not in the average is a huge influence as to whether the average is 0.14 or 0.07.
Aside: if you run the expected value estimate a few thousand times or more it just gets crazier; sometimes the expected value is actually negative if we just by luck get more than one sample in this critical region.
I contrived this example to produce occasional “black swan events“; obviously, our naïve algorithm for computing expected value does not take into account the difficulty of sampling a black swan event, and therefore produces inaccurate and inconsistent results.
Next time on FAIC: We know how to solve this problem exactly for discrete distributions; can we use some of those ideas to improve our estimate of the expected value in this scenario?

I remember dimly that this happened in the real world. In “ascent of money” the author showed that a “investment” firm was extremely sucessfull using data driven investment. Then the gulf war I happened, interest rates and volatility shot up and they lost boatloads of money.
They sampled only the last ~20 years or so, and that period did not include major upheavals.
As a political scientist turned programmer, I am always sceptical of our ability to use historical data to predict the future. Predicting tomorrow? Sure. Next week? Most probably. Next year …maybe.
We are simply not good at predicting our own future – predicting tectonic shifts like the rise of the brexit campaign for example is next to impossible. Include black swans events (a madman assasinating an arch duke for example) and you get something like weather prediction: short term predictions can be accurate, but long term the weather will be different in unknown ways.
I totally agree. The most important thing I know about psychology is: we have a powerful bias towards believing that how things are now is how they will continue to be.
This becomes a big problem when “how things are” is “we’re walking a little closer to the cliff edge every day because we’ve always walked a little closer to the cliff edge every day, and it was never a problem before”. But this is an algorithm for *finding the edge of a cliff by falling off it*.
We lost two fully-crewed space shuttles by following that algorithm. You’d think we would have learned after the first one, but no, that bias is very strong.
Predicting market is hard because the agents are constantly seeking out to exploit any noticeable regularity in it, destroying it in the process. Paeadoxically, the “gambler’s ruin” logic may actually predict it better: “Okay, the real estate prices have been constantly rising for the past ten years — that makes it very likely that they’ll crash next year, because surely that can’t go on forever!”.
Pingback: Dew Drop – May 29, 2019 (#2968) | Morning Dew
Pingback: Fixing Random, part 33 | Fabulous adventures in coding