A few episodes back I made a version of the Bernoulli distribution that took integer “odds”. That is, the distribution randomly produces either zero or one, and we can say “produce on average 23 zeros for every 17 ones” or whatever.
An obvious extension of this would be to produce 0, 1, or 2 randomly, similarly with some ratios: say, average 10 zeros, 11 ones, 5 twos out of each 26 samples in the long run. Of course, there’s no need to stop at three outputs; basically, we want the distribution of any number from 0 to n, with any integer ratios between them. This is a non-uniform discrete distribution; if a Bernoulli distribution is flipping an unfair coin, this is rolling an unfair n-sided die.
We’ve seen that we can do that by making an array with 10 zeros, 11 ones and 5 twos, and then calling ToUniform on that, but what if we wanted weights that were 437:563:501:499 or something? It seems wasteful to make an array with two thousand elements just to solve this problem.
Let’s try to write the code to solve this problem without thinking too hard about it, and see where we get stuck:
public sealed class WeightedInteger : IDiscreteDistribution<int>
{
private readonly List<int> weights;
public static IDiscreteDistribution<int> Distribution(
params int[] weights) =>
Distribution((IEnumerable<int>)weights);
public static IDiscreteDistribution<int> Distribution(
IEnumerable<int> weights)
{
List<int> w = weights.ToList();
if (w.Any(x => x < 0) || !w.Any(x => x > 0))
throw new ArgumentException();
if (w.Count == 1)
return Singleton<int>.Distribution(0);
if (w.Count == 2)
return Bernoulli.Distribution(w[0], w[1]);
return new WeightedInteger(w);
}
private WeightedInteger(List<int> weights)
{
this.weights = weights;
}
public IEnumerable<int> Support() =>
Enumerable.Range(0, weights.Count).
Where(x => weights[x] != 0);
public int Weight(int i) =>
0 <= i && i < weights.Count ? weights[i] : 0
No surprises there! This is all straightforward boilerplate code like we’ve seen before.
Exercise: There are a few places where we could be a little smarter; for instance, if all the weights are zero except one, then we could make a singleton distribution for that case as well. If the last weight is zero, we can discard that weight. Give it a shot.
The interesting question is: how do we implement Sample? It is by no means obvious, at least, not to me. Over the next few episodes, we’ll look at a number of techniques for solving this problem. Today: the “inverse” technique.
Long-time readers of my blog might at this point be remembering my 2012 article on the “inverse transform sampling” technique: “how do you generate a non-uniform random number when given a standard uniform distribution?” In brief:
- Get the probability distribution function.
- Integrate it to get the cumulative distribution — that is the function where c(x) is the probability that a sample is less than x.
- The cumulative distribution is monotone nondecreasing and always between 0 and 1, so it has an inverse which we call the quantile function. Find it.
- If you sample from a standard continuous uniform distribution and then apply the quantile function to the result, the sample will conform to the desired distribution.
The examples I gave in that article were continuous distributions, but this technique works equally well with discrete distributions. (For discrete quantities we call the “probability distribution” function the “probability mass” function, for no particularly good reason I’m aware of.) In our case today we can simply treat the mass function as a non-normalized distribution. Here’s the non-normalized mass function for weights 10, 11, 5.
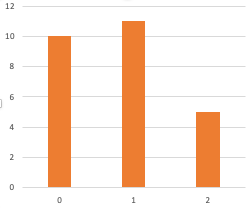
- Since the mass function is just a bunch of integer weights for integer values, the cumulative distribution function is a monotone step function, also from integers to integers. Here’s the cumulative distribution, which is 10, 21, 26. (That is, 10, 10+11, 10+11+5.)
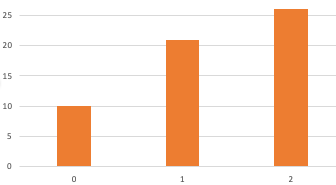
- The quantile function is the inverse of that function, which is another step function from integers to integers. Here’s the quantile function:
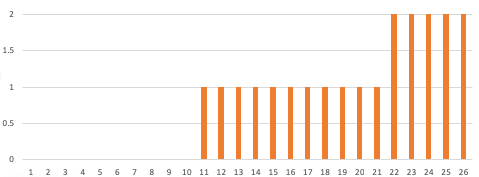
- We just evaluate that function at a uniformly random point, and we’re done. That is, we pick a uniform integer from 1 to 26, and look at the quantile function. If it is 1 through 10, we choose zero. If it is 11 through 21, we choose one, and if it is 22 through 26, we choose 2.
We get a number out from 0, 1 and 2 at the ratios of 10:11:5, as desired. And we did everything in integers; no pesky double arithmetic to get in the way. Are we done?
Sadly, no; the question is thoroughly begged! We already knew how to do that; we just create an array with ten zeros, eleven ones and five twos and sample from it. We’re trying to avoid that solution.
But maybe we can use these ideas to come up with a more efficient way to do the same thing.
The first thing we’ll do is compute the cumulative distribution in the constructor:
private readonly List<int> cumulative;
private WeightedInteger(List<int> weights)
{
this.weights = weights;
this.cumulative = new List<int>(weights.Count);
cumulative.Add(weights[0]);
for (int i = 1; i < weights.Count; i += 1)
cumulative.Add(cumulative[i – 1] + weights[i]);
}
So, if we start with weights 10, 11, 5, we have cumulative weights 10, 21, 26.
Again, remember what this means. Based on the weights, the probability of getting 0 is 10/26, the probability of getting 1 is 11/26, and the probability of getting 2 is 5/26. Therefore the probability of getting 0 or less is 10/26, the probability of getting 1 or less is 21/26, and the probability of getting 2 or less is 26/26. That’s how we compute the weights of the cumulative distribution.
Now we need to invert that cumulative distribution function. That is the function q(x) where q(1 to 10) = 0, q(11 to 21) = 1, q(22 to 26) = 2. We need to generate a random integer, and then compute this function, but how do we compute this function?
We generate a random number from 1 to 26, and then search the cumulative list for it. We’ll do a linear search for the leftmost bucket where the cumulative weight is not less than the sample:
public int Sample()
{
int total = cumulative[cumulative.Count – 1];
int uniform = SDU.Distribution(1, total).Sample();
int result = 0;
while (cumulative[result] < uniform)
result += 1;
return result;
}
You can verify for yourself that if we sample 1-10 we get 0, if we sample 11-21 we get 1, and if we sample 22-26 we get 2.
Is that it? Can it really be that easy? I think it can, but let’s try it out:
WeightedInteger.Distribution(10, 11, 5).Histogram()
0|************************************ 1|**************************************** 2|******************
Looking good!
Obviously it is O(n) to compute the cumulative weights, but we only have to do that once, in the constructor. The more worrisome problem is that searching for the result is O(n) in the number of weights.
If the number of weights is three or five or twenty, it’s probably not a problem. But if it’s a hundred or a thousand, a linear search is going to be problematic. (Then again, if it is more than a thousand, our assumption that discrete distributions have a small support is probably going out the window too.)
But of course we know how to improve the search time when we’re looking for an item in a sorted list; we can binary search it! As the documentation notes, the BinarySearch method of List returns “the zero-based index of item in the sorted list, if item is found; otherwise, a negative number that is the bitwise complement of the index of the next element that is larger than item…” which is exactly what we want.
- If we generate 10, 21 or 26 then we get the result we want immediately: 0, 1 or 2.
- If we generate 1 through 9, we get ~0, because cumulative[0] is larger
- similarly 11 through 20 gives us ~1
- similarly 22 through 25 gives us ~2
But ~ is its own inverse, so we can just ~ the result if negative and get the answer we want. Let’s implement it:
public int Sample()
{
int total = cumulative[cumulative.Count – 1];
int uniform = SDU.Distribution(1, total).Sample();
int result = cumulative.BinarySearch(uniform);
return result >= 0 ? result : ~result;
}
Seems legit.
Right?
Hmm.
Exercise: There’s a bug in the code above. Do you see it?
Give it some thought and then scroll down.
.
.
.
.
.
.
.
.
.
Since we are no longer looking “from the left”, we can accidentally choose a bucket that has a zero probability. For example, if our weights are 10, 0, 0, 11, 5, then the cumulative weights are 10, 10, 10, 21, 26. If 10 is our uniform sample then we must ensure that the binary search finds the leftmost 10 and says “0”, and not “1” or “2”.
There are a variety of techniques you could employ to solve this problem efficiently, and I’m not going to dig into them here. Give it a shot!
Let’s assume that we managed to solve our binary searching bug. This reduces our cost from O(n) to O(log n) which is very good, and for practical purposes, probably good enough. After all, with a thousand weights, that’s at most 10 comparisons, which should be pretty quick.
However, let’s think about some pathological cases.
Suppose we have a probability distribution with a thousand elements, distributed like this: 1, 1, 1, 1, 1, …. 1, 1001. The cumulative distribution will be 1, 2, 3, … 999, 2000. But 50% of the time on average we will uniformly generate a number greater than 999 and less than 2000, so 50% of the time our binary search will have to do all ten comparisons to discover that the rightmost bucket is the one we want. Can we do better?
Yes we can. Instead of building a list and binary searching that, we could build an optimal binary search tree and search that. We know ahead of time the probability of choosing each element in the binary search tree, so we can move the most common buckets towards the root of the tree, and then build a balanced binary search tree for the uncommon items in the leaves; there is an O(n2) algorithm for doing so, but I’m not going to show it here; see the Wikipedia article for details.
Alternatively, we could use a self-tuning binary tree such as a splay tree, and have it reorganize itself so that the most commonly searched for buckets appear near the root.
If we pursued this option of building a binary search tree, we could also prune zero-probability buckets from the tree entirely, eliminating the problem I mentioned above of accidentally finding a zero-probability bucket.
By using these techniques, we can get the average time spent sampling very low indeed, even for pathological cases, but it will still take longer to sample as the number of weights increases. (And we have a potentially difficult quadratic algorithm to build the optimized tree, though that only happens once.) Can we find a simple algorithm where the sample time is constant no matter how many weights there are?
Next time on FAIC: We’ll make two more attempts to find a more efficient sampling technique for this distribution.

I’m actually a bit surprised that BinarySearch doesn’t specify which equal item you get. The equivalent standard library functions in Python (bisect.bisect_left and bisect.bisect_right) and C++ (std::lower_bound and std::upper_bound) are specific about this, though perhaps a bit harder to use. I wonder if that’s why .NET opted for this API? It just feels odd to me, the mix of the low-level, specialised algorithm (user assumes responsibility to assure list order) and the only-cover-the-simplest-case approach.
I’m often surprised at the choices made by the BCL team as to what to include; I seem to spend a lot of my time re-implementing stuff that is pretty trivial but also of general usefulness.
I’ve made the argument in the past that “if it’s so easy to implement, just do it yourself”, and let the BCL team do the hard stuff, but I must say, it seems super weird to me that “MinBy” is in the F# standard library and not System.Linq.Enumerable, for instance.
Then again, we’re talking here about a language and runtime that took fifteen years to get around to adding value-typed *tuples*, for heaven’s sake, so maybe I should be not so surprised.
Pingback: Dew Drop – February 22, 2019 (#2905) | Morning Dew
Pingback: Fixing Random, part 8 | Fabulous adventures in coding
HI Eric! I’m new to your blog, and really enjoying this series.
However, I’m surprised that the code samples are limited to < 670px in width, causing lots of line wrapping. I've found the following much easier to read:
#page {
max-width: 1000px;
}
#content article .entry-content {
width: auto;
}
body {
color: black;
}