Code for today’s episode can be found here. I’ve added drag scrolling to the user interface, so if you click and hold, you can move around the grid much the same way that you’d move around an online map site.
Thanks to Java language designer Brian Goetz for being the first to suggest this episode’s topic. A number of other commenters here and on Twitter have suggested this and similar techniques; I will present a slightly simplified C# implementation of the algorithm today, and then next time I’ll discuss the performance implications, including those of using specialized hardware.
For the last few episodes we’ve been digging into the naïve algorithm: make an array of bools — or, in our rewrite, bytes — examine each neighbor of each cell, and fill in the new array accordingly. We’ve done some basic performance optimizations and managed to get it to about 1250 steps per second on an 8-quad, which seems pretty good.
Today I’m going to take a look at an approach that is similar in effect — we’re still going to have a byte array the size of the grid, and we’re still going to count the neighbors of each cell, but the order in which we do the operations and how we carry them out is going to be completely different.
The algorithm that I’m going to present here was developed by noted APL programmer, the late John Scholes. The original implementation of this algorithm is a single line:
life ← {⊃1 ⍵ ∨.∧ 3 4 = +/ +⌿ ¯1 0 1 ∘.⊖ ¯1 0 1 ⌽¨ ⊂⍵}
APL is a famously difficult language to understand because it is written in its own extraordinarily terse notation. I am not going to attempt to unpack this implementation! If you want an explanation, you can watch John Scholes explain it himself in this video:
Or, what I found more clear, is to follow along slowly in this article.
Rather than try to explain how this works in APL, I’m simply going to develop an algorithm that is in spirit pretty much the same as the one Scholes presents. It will differ in the implementation details — I’ll discuss how in the next episode — and will certainly be easier to read for the non-APL programmer. But the basic idea will be the same.
The key to understanding what is going on here is to first take a step back and understand what APL is for in the first place. It is a language for expressing algorithms that operate on multidimensional arrays. Since we’ve seen that we can implement a subset of the infinite Life grid in a 2-d array of bytes, each of which is 0 or 1, it seems plausible that a language specifically designed for array operations should be able to handle Life no problem.
APL can of course handle arbitrarily complex tensors, but we won’t need that machinery for the purposes of this discussion; all we need is a 2-d array of bytes. Thus I’m going to start by making my own “2-d array of bytes” type; it will be a class that is just a thin wrapper around a 1-d byte array. (We’ll see why I prefer the underlying implementation to be a 1-d byte array in a minute.)
class ByteBlock
{
private int Width { get; }
private int Height { get; }
private readonly byte[] bytes;
public ByteBlock(int width, int height, byte[] bytes = null)
{
this.Width = width;
this.Height = height;
this.bytes = bytes == null ? new byte[width * height] : bytes;
}
Obviously I’ve omitted error detection and whatnot for the purposes of keeping it short on the blog.
For the majority of the operations I’m going to perform on this type, byte blocks will be immutable. However it is convenient to be able to edit one without creating a bunch of garbage blocks, so I’ve added a getter and a setter; I’ll omit the details as they are very obvious. See the source code if you’re interested.
So far there is nothing out of the ordinary, but now let’s make it slightly more interesting. I want to add eight operations to this type, starting with “move left”:
1 2 3 2 3 0 4 5 6 ---move left--> 5 6 0 7 8 9 8 9 0
That is: “move left” produces a new byte block with the same size, but all the entries shifted one space left. The space left behind is filled in with zeros. (Again, this is slightly different from the APL vector rotation operation described by Scholes, and I’ll discuss why that is in an upcoming episode. I don’t want this first explanation to be overwhelmed by digging into subtleties.)
How can we implement that? Well, we have a one-dimensional array underlying this thing, so let’s just copy everything one unit to the left, and then fill in the zeros where we need to!
public ByteBlock MoveLeft()
{
byte[] newBytes = new byte[bytes.Length];
Array.Copy(bytes, 1, newBytes, 0, bytes.Length - 1);
for (int i = Width - 1; i < newBytes.Length; i += Width)
newBytes[i] = 0;
return new ByteBlock(Width, Height, newBytes);
}
Easy peasy. Now do exactly the same for MoveRight, MoveUp and MoveDown; the code is straightforward and so I’ll skip posting it here.
APL of course has a fully featured library of these sorts of array transformations, being an array language, but I just need four more.
“Where” takes a value and produces a new block which is one everywhere the original block has that value and zero everywhere else:
1 2 3 0 0 0 4 5 6 ---where 4--> 1 0 0 7 8 9 0 0 0
public ByteBlock Where(byte b)
{
byte[] newBytes = new byte[bytes.Length];
for (int i = 0; i < bytes.Length; i += 1)
newBytes[i] = bytes[i] == b ? (byte)1 : (byte)0;
return new ByteBlock(Width, Height, newBytes);
}
I need “and” and “or” operators that take two byte arrays of the same size and do the appropriate operation on each corresponding element of each array. And I need a “sum” operator that takes any number of byte arrays of the same size and produces the array that is the sum of each element.
I’ll make Sum an instance method that takes a param array of additional summands, and make the bitwise operators via operator overloading. You see how this goes; I don’t need to spell it all out; see the code on GitHub if you care about the details.
Once we have these tools, what do we do?
A Life grid is exactly the same as it was in the optimized naïve implementation: a 2-d array of bytes where each byte is 1 if the cell is alive and 0 if it is off, but this time we’re going to represent the cells as a byte block:
class Scholes : ILife
{
private const int height = 256;
private const int width = 256;
private ByteBlock cells;
public Scholes()
{
Clear();
}
public void Clear()
{
cells = new ByteBlock(width, height);
}
Pretty straightforward. I’ll skip the boilerplate getter/setter code and get straight to the crux of the matter: how does Next work?
The article I linked to above does a great job of explaining by running a simple example, so I’m going to do exactly the same thing; don’t mess with success. The R-pentomino is the smallest original configuration that runs for a long time before it gets to a stable configuration of still lifes, oscillators and gliders. The initial state is:
And one tick later:
It then takes 1103 ticks to settle down, but we’ll just worry about the first two. This is a good example because it has almost every case in it: we have living cells with 2 and 3 living neighbors that survive, we have living cells that die from overcrowding, and we have dead cells that stay dead and dead cells that come alive. (Though as we will see in a moment, there is a slightly different reason why this is a good test case!)
I’ll just focus on the 5×5 subset of the grid centered on the pentomino, and for compactness I’ll remove all the spacing between the grid values; none will ever go over nine. So we start with:
cells: 00000 00110 01100 00100 00000
You know what? That’s hard to read. I’m going to replace the zeros with dots, as in the video I linked above:
cells: ..... ..11. .11.. ..1.. .....
The first thing we do is move it up, down, left and right, or, if we think of this as if we were reading a standard map, we moved them west, east, north and south:
var w = cells.MoveLeft(); var e = cells.MoveRight(); var n = cells.MoveUp(); var s = cells.MoveDown(); w e n s ..... ..... ..11. ..... .11.. ...11 .11.. ..... 11... ..11. ..1.. ..11. .1... ...1. ..... .11.. ..... ..... ..... ..1..
Next thing we do is do an additional two moves on the “east” and “west” blocks; effectively these have moved the original pattern to the northwest, northeast, southwest and southeast if we think of it as a map.
var nw = w.MoveUp(); var ne = e.MoveUp(); var sw = w.MoveDown(); var se = e.MoveDown(); nw ne sw se .11.. ...11 ..... ..... 11... ..11. ..... ..... .1... ...1. .11.. ...11 ..... ..... 11... ..11. ..... ..... .1... ...1.
Now sum all of those eight new block with the original block.
var sum = cells.Sum(w, e, n, s, nw, ne, sw, se); 01221 13431 14541 13320 01110
All right, what have we got? We have an array where every entry in it is equal to the original value plus the count of all the living neighbors! The sum in the very middle, 5, for instance, is 1, the original value of the cell, plus the number of living neighbors, 4.
Now that we have this information, what can we do with it? We observe:
- If a cell was alive and it had two living neighbors, the sum is 3, and it will be alive on the next tick.
- If a cell was alive and it had three living neighbors, the sum is 4, and it will be alive on the next tick.
- If a cell was dead and it had three living neighbors, the sum is 3, and it will be alive on the next tick.
- Everything else is dead on the next tick.
(And now we see why I said before that this was a good test case; we have sums of both three and four on cells that were alive and dead previously.)
We have everything we need to make it happen. All the cells where sum is 3 are alive:
var threes = sum.Where(3); ..... .1.1. ..... .11.. .....
All the cells where the sum is 4 and the original cell was alive are alive:
var fours = sum.Where(4); var livingFours = fours & cells; ..... ..1.. .1... ..... .....
Finally…
cells = threes | livingFours; ..... .111. .1... .11.. .....
And we’re done!
(Technically I guess we didn’t really need “or” because the threes and living fours arrays are necessarily disjoint; we could have just summed them. But I think conceptually it makes good sense to think of this as an “or” rather than a sum.)
Let’s put it all together; it’s not nearly as concise as APL because nothing is, but it is pretty short:
public void Step()
{
var w = cells.MoveLeft();
var e = cells.MoveRight();
var n = cells.MoveUp();
var s = cells.MoveDown();
var nw = w.MoveUp();
var ne = e.MoveUp();
var sw = w.MoveDown();
var se = e.MoveDown();
var sum = cells.Sum(w, e, n, s, nw, ne, sw, se);
cells = sum.Where(3) | sum.Where(4) & cells;
}
I find it really quite pleasant to read the algorithm like this.
There are numerous other ways to use this same sort of technique to get what we want, of course; user yurivkhan pointed out in a comment to episode six that if we add a “multiply by scalar” operation that multiplies each value in a byte array by the same value, then this is the same computation just expressed a different way:
var sum = (cells * 8).Sum(w, e, n, s, nw, ne, sw, se); cells = sum.Where(3) | sum.Where(10) | sum.Where(11);
( I’ll address yurivkhan’s further comments about image processing techniques in the next episode.)
Next time on FAIC: We’ll look at the asymptotic, memory and time performance of this algorithm and its implementation, and discuss how ideas from image processing can improve the raw speed.

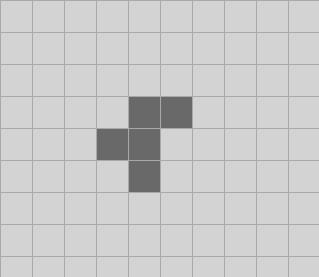
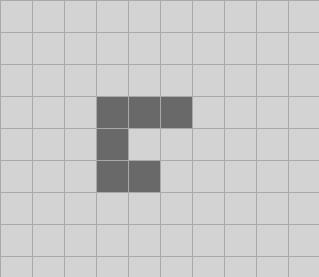
But if we have a “rectangle of death”, then we can avoid modifying `newBytes` in `MoveLeft` implementation (these bytes will already be set to zero because they were copied from the rectangle of death). Same goes for `MoveRight`, `MoveUp` and `MoveDown`.
And if they are not modified, there is no need in allocating 8 new byte arrays (and copying some data there from the old array), we can use the original array simply with the required offset (1 for MoveLeft, -1 for MoveRight, n for MoveUp and -n for MoveDown).
First off, both your comments are completely correct. Taking them in reverse order:
Regarding re-using arrays: Good insight. I’ll talk a little bit about the fact that we could have used offset techniques as an optimization briefly in part 8, but I will not actually implement any of them.
The first comment, about the “rectangle of death”, needs a little unpacking.
The idea as you note, is that if you know that there are all dead cells on the edge, then when you do a left or right shift you do not need to zero out the dead cells on the left or right edge because there are already zeros where you need them. But the problem with this approach then is: *the edge cells don’t stay dead*! If a cell on an edge happens to have exactly three neighbours, which is easy enough, then it comes alive, and now you don’t have a rectangle of dead edge cells anymore for the *next* round.
Of course you can always zero out the edges before (or after) every round, but that is then just moving the expense out of the shift and into the code that runs before the shift, so it’s not actually a savings.
Pingback: The Morning Brew - Chris Alcock » The Morning Brew #2990
Pingback: Life, part 8 | Fabulous adventures in coding
Pingback: Life, part 8 | Au moelleux