Introducing Bean Machine Graph
Bean Machine has many nice properties:
- It is integrated with Python, a language often used by data scientists
- It describes models using the rich, flexible pytorch library
- Inference works well even on models where data is stored in large tensors
I’m not going to go into details of how Bean Machine proper implements inference, at least not at this time. Suffice to say that the implementation of the inference algorithms is also in Python using PyTorch; for a Python program it is pretty fast, but it is still a Python program.
We realized early on that we could get order-of-magnitude better inference performance than Bean Machine’s Python implementation if we could restrict values in models to (mostly) single-value tensors and a limited set of distributions and operators.
In order to more rapidly run inference on this set of models, former team member Nim Arora developed a prototype of Bean Machine Graph (BMG).
BMG is a graph-building API (written in C++ with Python bindings) that allows the user to specify model elements as nodes in a graph, and relationships as directed edges. Recall that our “hello world” example from last time was:
@random_variable
def fairness():
return Beta(2,2)
@random_variable
def flip(n):
return Bernoulli(fairness())
That model written in BMG’s Python bindings would look like this: (I’ve omitted the queries and observations steps for now, and we’ll only generate one sample coin flip instead of ten as in the previous example, to make the graph easier to read.)
g = Graph()
two = g.add_constant_pos_real(2.0)
beta = g.add_distribution(
DistributionType.BETA,
AtomicType.PROBABILITY,
[two, two])
betasamp = g.add_operator(OperatorType.SAMPLE, [beta])
bern = g.add_distribution(
DistributionType.BERNOULLI,
AtomicType.BOOLEAN,
[betasamp])
flip0 = g.add_operator(OperatorType.SAMPLE, [bern])
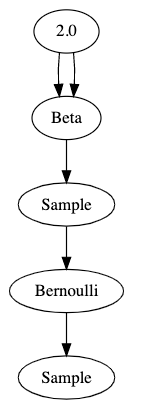
That’s pretty hard to read. Here’s a visualization of the graph that this code generates:
These graphs are properly called Bayesian network diagrams, but for this series I’m just going to call them “graphs”.
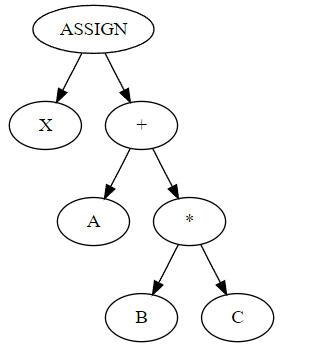
I should say a little about the conventions we use in this graphical representation. Compiler developers like me are used to decomposing programs into abstract syntax trees. An AST is, as the name suggests, a tree. ASTs are typically drawn with the “root” at the top of the page, arrows point down, “parent nodes” are above “child nodes”, and operators are parents of their operands. The AST for something like x = a + b * c would be
where X, A, B, C are identifier nodes.
Bayesian network diagrams are just different enough to be confusing to the compiler developer. First of all, they are directed acyclic graphs, not trees. Second, the convention is that operators are children of their operands, not parents.
The best way I’ve found to think about it is that graphs show data flow from top to bottom. The parameter 2.0 flows into an operator which produces a beta distribution — twice. That distribution flows into a sample operator which then produces a sample from its parent distribution. That sampled value flows into an operator which produces a Bernoulli distribution, and finally we get a sample from that distribution.
If we wanted multiple flips of the same coin, as in the original Python example, we would produce multiple sample nodes out of the Bernoulli distribution.
BMG also has the ability to mark sample nodes as “observed” and to mark operator nodes as “queried”; it implements multiple inference algorithms which, just like Bean Machine proper, produce plausible samples from the posterior distributions of the queried nodes given the values of the observed nodes. For the subset of models that can be represented in BMG, the performance of the inference algorithms can be some orders of magnitude faster than the Bean Machine Python implementation.
Summing up: Our team had two independent implementations of inference algorithms; Bean Machine proper takes as its input some decorated Python methods which concisely and elegantly represents models in a highly general way using PyTorch, but the inference is relatively slow. Bean Machine Graph requires the user to write ugly, verbose graph construction code and greatly restricts both the data types and the set of supported operators, but uses those restrictions to achieve large inference speed improvements.
Next time on FAIC: Given the above description, surely you’ve guessed by now what the compiler guy has been doing for the last three years on this team full of data scientists! Can we automatically translate a Bean Machine Python model into a BMG graph to get BMG inference performance without sacrificing representational power?

Pingback: The Morning Brew - Chris Alcock » The Morning Brew #3601